A field normally denoted 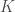 is an abstract structure that satisfies a list of axioms, these axioms are motivated by the algebraic properties of the rational numbers
is an abstract structure that satisfies a list of axioms, these axioms are motivated by the algebraic properties of the rational numbers  and other number systems such as the real numbers
and other number systems such as the real numbers 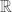 and the complex numbers
and the complex numbers 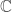 . With the privilege of being alive now rather than in the 1800s abstract mathematics, particularly abstract algebra, is widely taught and fields can just be considered as a set with a nice structure (I’m not trying to dumb down the concept but to emphasis that fields aren’t illusive and magical). In this post I will be talking a bit about Field extensions, Rings, Integral Domains and the structure of the integers as a ring. A quick warning: this post is rather long.
. With the privilege of being alive now rather than in the 1800s abstract mathematics, particularly abstract algebra, is widely taught and fields can just be considered as a set with a nice structure (I’m not trying to dumb down the concept but to emphasis that fields aren’t illusive and magical). In this post I will be talking a bit about Field extensions, Rings, Integral Domains and the structure of the integers as a ring. A quick warning: this post is rather long.
An extremely important concept in field theory, more generally ring theory, is the characteristic of such a structure denoted  . The characteristic is the first step in the direction to classify fields/rings as, informally, it tells you what the smallest subfield/ring our structure contains. More precisely we can map
. The characteristic is the first step in the direction to classify fields/rings as, informally, it tells you what the smallest subfield/ring our structure contains. More precisely we can map  into
into 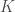 by
by 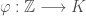 defined by
defined by 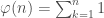 ,
, 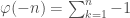 for
for  and
and  . This is a ring homomorphism and the kernel is an integral domain of
. This is a ring homomorphism and the kernel is an integral domain of  so it will be of the form
so it will be of the form 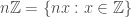 where
where  and using the first isomorphism theorem
and using the first isomorphism theorem  and as the image is an integral domain
and as the image is an integral domain  where
where 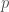 is prime or
is prime or  . We define the characteristic as this value so either
. We define the characteristic as this value so either  where
where  is prime or
is prime or  . Another way to think about the characteristic, is that it’s the smallest number of times you have to continuously add the multiplicative identity to get the additive identity.
. Another way to think about the characteristic, is that it’s the smallest number of times you have to continuously add the multiplicative identity to get the additive identity.
Throughout the rest of the post 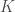 will be a finite field. With
will be a finite field. With 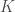 being finite it’s not hard to show it must have
being finite it’s not hard to show it must have  where
where 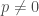 is prime. This follows by the short argument that if
is prime. This follows by the short argument that if  the field must contain
the field must contain  as a subring, this cant be so as
as a subring, this cant be so as  is infinite and hence so would
is infinite and hence so would 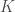 which gives us a contradiction. This tells us that
which gives us a contradiction. This tells us that 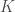 must contain the field
must contain the field  if
if  and it’s the smallest field
and it’s the smallest field 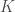 contains. Looking at the degree of the extension
contains. Looking at the degree of the extension ![[K : \mathbb{F}_P] = n](https://s0.wp.com/latex.php?latex=%5BK+%3A+%5Cmathbb%7BF%7D_P%5D+%3D+n+&bg=ffffff&fg=404040&s=0&c=20201002) (if you’re unfamiliar with this concept click here) we have
(if you’re unfamiliar with this concept click here) we have 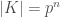 so we get a bit more information, the size of a finite field must be a power of a prime.
so we get a bit more information, the size of a finite field must be a power of a prime.
We’ll assume our finite field 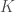 has
has 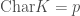 from now on and in doing so we have an endomorphism
from now on and in doing so we have an endomorphism  defined by
defined by  for each
for each  . This map is given a special name, the Frobenius endomorphism, and as all things with a name it’s important.
. This map is given a special name, the Frobenius endomorphism, and as all things with a name it’s important.
As we’ve assumed 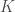 is finite we can in-fact conclude
is finite we can in-fact conclude  is an automorphism (This is not true for a general field). let
is an automorphism (This is not true for a general field). let 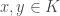 we calculate
we calculate  and by noticing
and by noticing  with
with  , using the binomial theorem and that our characteristic is
, using the binomial theorem and that our characteristic is  we calculate
we calculate 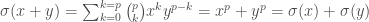 so
so  is a homomorphism and as the name suggests an endomorphism as
is a homomorphism and as the name suggests an endomorphism as 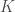 is closed under multiplication. As
is closed under multiplication. As 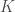 is finite to show
is finite to show  is bijective we only need to show the map is injective or surjective and it’s much easier to prove injectivity. Suppose
is bijective we only need to show the map is injective or surjective and it’s much easier to prove injectivity. Suppose  then
then 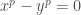 so by the fact we have a homomorphism
so by the fact we have a homomorphism  and as we are in an integral domain, in particular a finite field, we have
and as we are in an integral domain, in particular a finite field, we have  .
.
With all this setup we are in good shape to show what finite fields must look like and surprisingly there is only one such possibility. The result is stated in the theorem bellow and was first proved by E.H Moore in 1893.
Theorem: Let 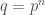 where
where 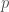 is prime, let
is prime, let  be an algebraically closed field with
be an algebraically closed field with  . There exists a unique subfield
. There exists a unique subfield  of
of  with
with  elements. This is the set of roots of the the polynomial
elements. This is the set of roots of the the polynomial  more explicit
more explicit  .
.
Proof of Theorem: We have  being algebraically closed with characteristic
being algebraically closed with characteristic  so we must have the map
so we must have the map  defined by
defined by  being an injective homomorphism as
being an injective homomorphism as  , think of
, think of  as the concatenation of
as the concatenation of 
 times. Note that it isn’t necessarily an isomorphism as
times. Note that it isn’t necessarily an isomorphism as  might not be finite. This means the fixed points of
might not be finite. This means the fixed points of  , the set
, the set  forms a subfield of
forms a subfield of  which is precisely
which is precisely  .
.
If we show that our set of fixed points has size  we are done as we’ve found our
we are done as we’ve found our  of size
of size  . This is equivalent to showing
. This is equivalent to showing  has
has  distinct roots in
distinct roots in  . We can easily argue that if
. We can easily argue that if  has roots they must be distinct as we observe if
has roots they must be distinct as we observe if ![f \in \Omega[x]](https://s0.wp.com/latex.php?latex=f+%5Cin+%5COmega%5Bx%5D+&bg=ffffff&fg=404040&s=0&c=20201002) has a ‘double’ root say
has a ‘double’ root say 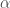 then
then 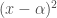 divides
divides 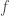 so the derivative of
so the derivative of 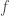 with respect to
with respect to  ,
, 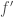 is non-constant but
is non-constant but 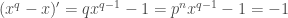 as
as  . This means all the roots are distinct and as we have assumed
. This means all the roots are distinct and as we have assumed  is algebraically closed so all
is algebraically closed so all  of them must exist.
of them must exist.
To show uniqueness we assume 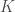 is a subfield of
is a subfield of  with exactly
with exactly  elements. Looking at the multiplicative group of units
elements. Looking at the multiplicative group of units  by definition there are
by definition there are  of them, by Lagrange’s Theorem for groups we have
of them, by Lagrange’s Theorem for groups we have  for
for 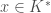 so
so 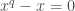 hence
hence  . Trivially we have
. Trivially we have  so
so  and as they both contain
and as they both contain  elements we have
elements we have  .
.
It follows directly from this theorem that all finite fields 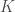 with
with 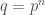 elements where
elements where  is prime is isomorphic to the
is prime is isomorphic to the  defined above. This follows from Zorn’s lemma allowing us to embed
defined above. This follows from Zorn’s lemma allowing us to embed 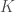 into an algebraically closed field
into an algebraically closed field  .
.
So there we have it.
-algebra
where
is a field, is a ring with the added structure of being a vector space over
(with respect to the same addition) where scalar multiplication behaves nicely with the ring multiplication.
for
and
. The atypical example is a matrix algebra of dimension
with matrix elements in
denoted
. There is a notion of algebra morphism which is not too hard to figure out with the above or a quick google, so we have a notion of isomorphism.
-dimensional matrix algebra these objects are the tuples
where
. As a collection, they are denoted
. These form a vector space and as algebras
. Where the algebra operation in
is matrix multiplication and
is the algebra of vector space automorphisms
with the algebra operation being composition.
-module can be found elsewhere but to motivate its origins, it is precisely the articulation of assigning some ‘vectors’ in some vector space
to a general
-algebra
which
can act on
similarly to matrices on tuples. If you struggle to remember the definition of an
-module just think like this and you should be able to reconstruct it.
, with the relaxation of the structure of a vector space. And so we can assign ‘vectors’ to rings by looking at
-modules. So we can ask the question, what are
-modules? These are in fact abelian groups (why?) and so the collection of possible ‘vectors’ for
can be thought of as just abelian groups.